はじめに
参考文献
予備知識
- 離散確率分布：ベルヌーイ分布とカテゴリ分布
  - クラスタ数2の場合：ベルヌーイ分布
  - クラスタ数Kの場合：カテゴリ分布
- 連続確率分布：ベータ分布とディリクレ分布
  - ベータ分布
  - ディリクレ分布
混合モデル

はじめに

須山ベイズ本を参考に，混合モデルの導入部分を勉強したノート．離散確率分布の復習も含む．隠れマルコフモデルについて学びたかったのだが，そのために混合モデルについて押さえようと思ったらそれなりのボリュームになってしまったので一旦記事としてまとめておく．

あくまでも勉強ノートなので，教科書ありきの文章である．これを解説として読んでもらうのではなく，須山本を読む上での補足資料として参考になれば幸いである．単なる写経ではなく，式変形は細かくやっていたりするので，そのあたり誰かの役に立つかもしれない．

参考文献

須山敦志，「機械学習スタートアップシリーズ　ベイズ推論による機械学習入門 (ＫＳ情報科学専門書) Kindle版」，講談社，2017.
- 良い評判しか目にしない名著．書籍版とKindle版両方とも買ってしまった．これ自体を教科書として勉強できると同時に，他の本を読むときの参考書としても強力なので，読みたいときにすぐ読めるKindle版便利．
Christopher M. Bishop. 2006. Pattern Recognition and Machine Learning (Information Science and Statistics). Springer-Verlag, Berlin, Heidelberg.
- いわゆるPRML．英語版はリンク先のとおりMicrosoftのサイトからダウンロードできます．日本語版は上巻しか持っておらず，上巻には混合モデルの話は含まれていない．全てが一体の英語版便利．
- 9章で混合モデルの話が扱われている．

機械学習スタートアップシリーズベイズ推論による機械学習入門 (KS情報科学専門書)

作者:須山敦志
発売日: 2017/10/21
メディア: 単行本（ソフトカバー）

Pattern Recognition and Machine Learning (Information Science and Statistics)

作者:Bishop, Christopher M.
発売日: 2006/08/17
メディア: ハードカバー

予備知識

離散確率分布：ベルヌーイ分布とカテゴリ分布

混合モデルでは，データを構成するこの点たちは分布1から発生しており，他の点たちは分布2から発生しており・・・と，複数の異なる分布によってデータが構成されていると考える．データがどの分布から発生したのか，ということを考えるのはいわゆるクラスタリング問題であり，このとき有用になるのがベルヌーイ分布とカテゴリ分布である．これらを予備知識として復習しておこう．ベルヌーイ分布は2つのクラスタのみを考えるケースであり，ベルヌーイ分布を $K$ 次元に拡張したものがカテゴリ分布である．すなわちカテゴリ分布は $K$ 個のクラスタのうち，どのクラスタに所属するのかを示す確率分布になっている．須山本ではカテゴリ分布と表記されているが，一般にはカテゴリカル分布と呼ばれるようである．マルチヌーイ分布という言い方もあるらしい．

クラスタ数2の場合：ベルヌーイ分布

まずベルヌーイ分布であるが， $0$ か $1$ のどちらかを取る二値変数 $x$ の生成分布である．これは $0$ から $1$ までの連続値を取るパラメータ $\mu\in(0,1)$ によって形が決まり，次のように書く．

\begin{align} {\rm Bern}(x|\mu)=\mu^x(1-\mu)^{1-x} \end{align}

$x=0$ のときは $(1-\mu)^{1}$ になるし， $x=1$ のときは $\mu^1$ になるから，これはつまり $\mu$ の値は $x=1$ が得られる確率そのものだ，ということである．冗長だが，折角なので具体的な数字を入れてどうなるか見ておこう． $\mu=0.5$ の場合を考えてみると， \begin{align} {\rm Bern}(x|0.5)=0.5^x\times0.5^{1-x} \end{align} となって， $x=0$ となる確率は ${\rm Bern}(0|0.5)=0.5^0\times0.5^{1}=0.5$ となる．逆に $x=1$ となる確率も \begin{align} {\rm Bern}(1|0.5)=0.5^1\times0.5^{0}=0.5 \end{align} となるから，この場合は $0$ と $1$ は半々の確率で得られるということになる．

クラスタ数Kの場合：カテゴリ分布

ベルヌーイ分布ではクラスタが2つの場合について考えたが， $K$ 個の場合はどう表せるだろうか．

ここで変数 $\boldsymbol{s}$ を考える（これは後々見るように，混合分布の文脈では直接観測に引っかからない潜在変数となる）．

このベクトルの要素は $s_k\in\{0,1\}$ ，すなわち $0$ か $1$ かどちらかの値を取る離散的な変数であり，かつ $\Sigma_{k=1}^Ks_k=1$ を満たす．つまり， $k$ 番目が $1$ であれば，他の要素は全て $0$ ということになる．このようにしてクラスタへの所属を表すことを $1$ of $K$ 表現と呼ぶ．

ベルヌーイ分布では1つのパラメータ $\mu\in(0,1)$ によって分布が決まっていた．カテゴリ分布では，これを $K$ 個に拡張して，混合比率 $\boldsymbol{\pi}=\left(\pi_1,\cdots,\pi_K\right)$ によって分布の形を決める． $\pi_k\in(0,1)$ であり， $\Sigma_{k=1}^K\pi_k=1$ を満たす． $s_k$ が離散変数であるのに対して， $\pi_k$ は連続値を取ることに注意しておこう．

以上で準備が整った．カテゴリ分布は，次のように書ける．

\begin{aligned} {\rm Cat}(\boldsymbol{s}|\boldsymbol{\pi})=\Pi _ {k=1}^{K} \pi _ {k}^{s _ {k}} \end{aligned}

クラスタ数 $K=2$ の場合について考えてみよう．このとき潜在変数は $\boldsymbol{s}=\{s_1, s_2\}=\{s_1, 1-s_1\}$ となるし，混合比率は $\boldsymbol{\pi}=\{\pi_1, \pi_2\}=\{\pi_1, 1-\pi_1\}$ である．したがって

\begin{align} {\rm Cat}(\boldsymbol{s}| \boldsymbol{\pi}) &= \Pi _ {k=1}^K \pi_k^{s _ k} \\ &= \Pi _ {k=1}^2 \pi_k^{s _ k} \\ &= \pi _ 1^{s _ 1}\cdot\pi_2^{s _ 2} \\ &= \pi _ 1^{s _ 1}\cdot(1-\pi _ 1)^{1-s _ 1} \end{align}

となって，ベルヌーイ分布に一致することが確かめられた． 2つのクラスタのうち，1番目のクラスタが選ばれる確率を計算したいなら， $\boldsymbol{s}=\{s_{1}, s_{2}\}=\{1, 0\}$ だから，

\begin{align} {\rm Cat}(\boldsymbol{s}|\boldsymbol{\pi}) &= \pi _ 1^{s _ 1}\cdot(1-\pi _ 1)^{1-s _ 1} \\ &=\pi _ 1^{1}\cdot(1-\pi _ 1)^{0} \\ &=\pi _ 1 \end{align}

となって $\pi_1$ が残る． $s_1$ と $s_2$ が半々の確率で選ばれる場合， $\pi_1=0.5$ である．ベルヌーイ分布と同様に，結局 $\boldsymbol{\pi}$ によって $\boldsymbol{s}$ の各要素が出現する確率が決まることが確認できた．

連続確率分布：ベータ分布とディリクレ分布

カテゴリ分布を決めるのは混合比率 $\pi_k\in(0,1)$ であった．次はこの $\pi$ を得る確率について考えたい． $\pi$ は $0$ から $1$ までの値を取る連続変数であり，このような変数を生成する確率分布がベータ分布とディリクレ分布である．今回は知識として眺めるだけに留めておく．「そういうもん」と思って欲しい．

ベータ分布

ベルヌーイ分布で出て来た $\mu\in(0,1)$ の分布を与えてくれるのがベータ分布である．パラメータ $a$ と $b$ を使って次のように書く． ${\rm Beta}(\mu|a,b)=C_B(a,b)\mu^{a-1}(1-\mu)^{b-1}$ $C_B(a,b)$ は $a$ と $b$ の値に応じて決まる規格化係数で，ガンマ関数によって構成される．

ディリクレ分布

カテゴリ分布で出て来た混合比率 $\pi_k\in(0,1)$ の分布を与えてくれるのがディリクレ分布である．パラメータ $\boldsymbol{\alpha}$ を使って次のように書く．

\begin{align} {\rm Dir}(\boldsymbol{\pi}|\boldsymbol{\alpha}) =C _ D(\boldsymbol{\alpha})\Pi _ {k=1}^K \pi_k^{\alpha _ k-1} \end{align}

規格化係数 $C_D(\boldsymbol{\alpha})$ はやはりガンマ関数によって構成される．

混合モデル

混合モデルでは，データが複数の異なる分布によって生成していると考える．データを生成する確率分布の個数（クラスタ数）を $K$ として， $N$ 個のデータ $\boldsymbol{X}=\{\boldsymbol{x_1},\cdots, \boldsymbol{x_N} \}$ の生成過程を考えよう．ちなみに， $\boldsymbol{X}$ の1点である $\boldsymbol{x_n}$ は多次元空間上の1つの点であり，これ自体がベクトルである．たとえば，3次元空間上にばらまかれている点の集団がデータ $\boldsymbol{X}$ であれば，その一つ一つの点は3次元ベクトルであって $\boldsymbol{x _ n}=(x _ {n,x},x _ {n,y},x _ {n,z})^T$ のように書ける．以下では混合モデルを考える上で道具となる量について見ていく．

クラスタの混合比率 $\pi$

データのうち，それぞれの分布（クラスタ）がどの程度含まれているか， $0$ から $1$ までの値で表すことにする．これをベクトルとしてまとめたものが混合比率（mixture weight） $\pi$ である． $\boldsymbol{\pi}=\left(\pi _ 1,\cdots,\pi _ K\right)^T$ ここで $\pi_K\in(0,1)$ である．また全体で $1$ となるように $\Sigma_{k=1}^K\pi_k=1$ とする．さて，予備知識のところで見たように， $\pi$ は"混合比率"なのだから， $0$ から $1$ までの連続値を取ることに注意しておこう．これに対して，この後出てくる潜在変数 $s$ はどのクラスタに属するかを $0$ か $1$ で表す離散的な量である．基本的なことではあるが確認のため記しておくと，このような離散的な集合は波括弧を用いて $\{\cdot\}$ で表す．何でこんなことをくどくど書くのかというと，単に私の脳が混乱したからにすぎない． $\boldsymbol{\pi}$ も確率変数であって，事前分布 $p(\boldsymbol{\pi})$ に従って生成されるとする．

モデルパラメータ $\theta$

たとえば各分布が正規分布の場合，平均値と分散がモデルパラメータとなる．分布ごとにパラメータは異なるから， $k$ 番目の分布のパラメータセットをベクトル $\boldsymbol{\theta}_k$ で表す．正規分布の場合であれば， $\boldsymbol{\theta} _ k=\mathcal{N}\left(\mu _ k, \sigma _ k\right)$ となる． $\boldsymbol{\theta} _ k$ は事前分布 $p(\boldsymbol{\theta} _ k)$ に従って生成されるとする．

潜在変数 $s_n$

観測データ $\boldsymbol{X}=\{\boldsymbol{x_1},\cdots, \boldsymbol{x_N} \}$ のある点 $\boldsymbol{x_n}$ が $K$ 個の分布のうちどれによって生成するかという対応関係を決める変数が $s_n$ であり，潜在変数と呼ばれる． $s_n=\{s_{n,1}, \cdots, s_{n,K}\}$ であり，予備知識で見たとおり $1$ of $K$ 表現によってどのクラスタに所属しているかを表す．これが $N$ 個分あるのだから，その集合を $\boldsymbol{S}=\{\boldsymbol{s} _ 1, \cdots, \boldsymbol{s} _ N\}$ と表す．また，データがどのクラスタに所属しているか（どのクラスタから生成したか）？というのは，そのデータがどのモデルパラメータに対応しているのかを考えることと同じである．

グラフィカルモデル

ここで考えているデータの生成過程は下に示すグラフィカルモデルで表すことができる．

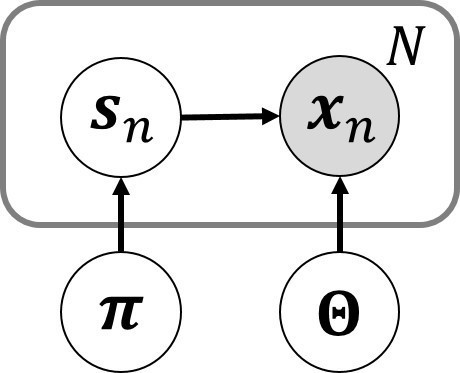
$\boldsymbol{x} _ n$ は $\boldsymbol{\Theta}$ と $\boldsymbol{s} _ n$ に依存する．注意しておくべきなのは， $\boldsymbol{\Theta}$ と $\boldsymbol{s} _ n$ の間には依存関係が無いということ．各クラスタの分布がどのような形になっているかということ（ $\boldsymbol{\Theta}$ ）と，どの分布が選ばれるかということ（ $\boldsymbol{s} _ n$ ）は無関係である．

余談であるが，図のように $N$ 個の量を一つのノードで表し，それらを四角で囲ってから個数を $N$ と記す省略表記方法はプレート表現（plate notation）と言われる．また， $\boldsymbol{x}_n$ が観測値であることはノードを塗りつぶすことによって示す．このあたりは須山本p.24や，PRMLの8章で解説がなされている．

混合分布の構成

$\boldsymbol{x} _ n$ がどのクラスタ（モデルパラメータ）に属するかは潜在変数 $s _ n$ で決まるのであった． $\boldsymbol{x} _ n$ は $s _ n$ とモデルパラメータ全体の集合 $\boldsymbol{\Theta}=\{\boldsymbol{\theta} _ 1,\cdots\boldsymbol{\theta} _ k\}$ に依存して決まるので， $\boldsymbol{x} _ n$ の生成確率は $p(\boldsymbol{x} _ n|s_n,\boldsymbol{\Theta})$ と書ける．予備知識として見たように， $K$ 個のクラスタについてのカテゴリ分布は次のように書けるのだった．

\begin{align} {\rm Cat}(\boldsymbol{s}|\boldsymbol{\pi})=\Pi _ {k=1}^K \pi _ k^{s _ k} \end{align}

これを参考にして， $\boldsymbol{x}_n$ の生成確率は次のように書ける．

\begin{align} p(\boldsymbol{x} _ n|s _ n,\boldsymbol{\Theta})=\Pi _ {k=1}^K p(\boldsymbol{x} _ n|\boldsymbol{\theta} _ k)^{s _ {n,k}} \end{align}

となる．くどいようだが，やはりひとまず具体的に見ていこう． $K=2$ の場合を考えると， $\boldsymbol{s}_n=\{s_{n,1}, s_{n,2}\}=\{s_{n,1}, 1-s_{n,1}\}$ なんだから，

ということである． $\boldsymbol{x}_n$ が1番目のクラスタから生成されたとすると， $\boldsymbol{s}_n=\{s_{n,1}, s_{n,2}\}=\{1, 0\}$ だから，

\begin{align} p(\boldsymbol{x} _ n|s _ n,\boldsymbol{\Theta}) &=\Pi _ {k=1}^2 p(\boldsymbol{x} _ n|\boldsymbol{\theta} _ k)^{s _ {n,k}} \\ &=p(\boldsymbol{x} _ n|\boldsymbol{\theta} _ 1)^{s _ {n,1}}\cdot p(\boldsymbol{x} _ n|\boldsymbol{\theta} _ 2)^{1-s _ {n,1}} \\ &=p(\boldsymbol{x} _ n|\boldsymbol{\theta} _ 1)^{1}\cdot p(\boldsymbol{x} _ n|\boldsymbol{\theta} _ 2)^{0} \\ &=p(\boldsymbol{x} _ n|\boldsymbol{\theta} _ 1) \end{align}

となって $p(\boldsymbol{x} _ n|\boldsymbol{\theta} _ 1)$ が残る． $p(\boldsymbol{x} _ n|\boldsymbol{\theta} _ k)$ はあるモデルパラメータを選んだときに $\boldsymbol{x}\ _ n$ が得られる確率である．モデルが正規分布だとすればモデルパラメータは $\boldsymbol{\theta} _ k=\{\boldsymbol{\mu} _ k, \boldsymbol{\Sigma } _ k\}$ であり， $k=1,\cdots,K$ に対して，

\begin{align} p(\boldsymbol{x} _ n|\boldsymbol{\theta} _ k) = \mathcal{N}(\boldsymbol{x} _ n|\boldsymbol{\mu} _ k, \boldsymbol{\Sigma} _ k ) \end{align}

となる．

さて，潜在変数 $s$ が $1$ であるか $0$ であるかの確率は混合比率 $\pi$ で決まり，

\begin{align} {\rm Cat}(\boldsymbol{s}|\boldsymbol{\pi})=\Pi _ {k=1}^K \pi _ k^{s _ k} \end{align}

だった．そして $\pi _ 1$ が $0.5$ か， $0.1$ かといったように， $\boldsymbol{\pi}$ の各要素がどのような値を取るかというのは事前分布 $p(\boldsymbol{\pi})$ によって決まると考えるのだった．この事前分布としてディリクレ分布を使う．すなわち $p(\boldsymbol{\pi})={\rm Dir}(\boldsymbol{\pi}|\boldsymbol{\alpha})$ である．

同時分布

以上で下準備が終わった．それでは $N$ 個のデータ $\boldsymbol{X}=\{\boldsymbol{x\ _ 1},\cdots, \boldsymbol{x\ _ N} \}$ ，潜在変数 $\boldsymbol{S}=\{\boldsymbol{s} _ 1, \cdots, \boldsymbol{s} _ N\}$ ，モデルパラメータ $\boldsymbol{\Theta}=\{\boldsymbol{\theta} _ 1,\cdots\boldsymbol{\theta} _ k\}$ ，混合比率 $\boldsymbol{\pi}=\left(\pi\ _ 1,\cdots,\pi\ _ K\right)^T$ の同時分布 $p(\boldsymbol{X},\boldsymbol{S},\boldsymbol{\Theta},\boldsymbol{\pi})$ を考える．乗法定理によって条件付き分布に書き換えていくと，

\begin{align} p(\boldsymbol{X},\boldsymbol{S},\boldsymbol{\Theta},\boldsymbol{\pi}) &= p(\boldsymbol{X},\boldsymbol{S},\boldsymbol{\Theta}|\boldsymbol{\pi})p(\boldsymbol{\pi}) \\ &= p(\boldsymbol{X},\boldsymbol{\Theta}|\boldsymbol{S},\boldsymbol{\pi})p(\boldsymbol{S}|\boldsymbol{\pi})p(\boldsymbol{\pi}) \\ &= p(\boldsymbol{X}|\boldsymbol{S},\boldsymbol{\Theta}, \boldsymbol{\pi})p(\boldsymbol{\Theta}|\boldsymbol{S},\boldsymbol{\pi})p(\boldsymbol{S}|\boldsymbol{\pi})p(\boldsymbol{\pi}) \\ \end{align}

ここでグラフィカルモデルを思い出す．

図から明らかなように， $\boldsymbol{\Theta}$ と $\boldsymbol{s} _ n$ の間には依存関係が無い． $\boldsymbol{\Theta}$ は $\boldsymbol{s} _ n$ にも $\boldsymbol{\pi}$ にも無関係なのだから，上の同時分布の式で出て来た $p(\boldsymbol{\Theta}|\boldsymbol{S},\boldsymbol{\pi})$ は，単なる $p(\boldsymbol{\Theta})$ に等しい．つまり，

\begin{align} p(\boldsymbol{\Theta}|\boldsymbol{S},\boldsymbol{\pi}) = p(\boldsymbol{\Theta}) \end{align}

である．もう一つ，図から明らかなように， $\boldsymbol{x} _ n$ は $\boldsymbol{\Theta}$ と $\boldsymbol{s} _ n$ に依存するけれど $\boldsymbol{\pi}$ には直接依存しない．したがって，

\begin{align} p(\boldsymbol{X}|\boldsymbol{S},\boldsymbol{\Theta}, \boldsymbol{\pi}) = p(\boldsymbol{X}|\boldsymbol{S},\boldsymbol{\Theta}) \end{align}

となる．というわけで同時分布の式は，次のように書き換えられる．

ここで， $p(\boldsymbol{X}|\boldsymbol{S},\boldsymbol{\Theta})$ は

であって， $\boldsymbol{x} _ n$ は $\boldsymbol{S}$ のうち $\boldsymbol{s} _ n$ にしか依存しないということを考慮すると，

\begin{align} p(\boldsymbol{X}|\boldsymbol{S},\boldsymbol{\Theta}) &= p(\boldsymbol{x} _ 1,\cdots, \boldsymbol{x} _ N|\boldsymbol{s} _ 1,\cdots, \boldsymbol{s} _ N,\boldsymbol{\Theta}) \\ &=p(\boldsymbol{x} _ 1|\boldsymbol{s} _ 1,\cdots, \boldsymbol{s} _ N,\boldsymbol{\Theta}) \cdots p(\boldsymbol{x} _ N|\boldsymbol{s} _ 1,\cdots, \boldsymbol{s} _ N,\boldsymbol{\Theta}) \\ &=p(\boldsymbol{x} _ 1|\boldsymbol{s} _ 1,\boldsymbol{\Theta}) \cdots p(\boldsymbol{x} _ N|\boldsymbol{s} _ N,\boldsymbol{\Theta}) \\ &= \Pi _ {n=1}^N p(\boldsymbol{x} _ n|\boldsymbol{s} _ n,\boldsymbol{\Theta}) \end{align}

$p(\boldsymbol{S}|\boldsymbol{\pi})$ についても同様．

\begin{align} p(\boldsymbol{S}|\boldsymbol{\pi}) &= p(\boldsymbol{s} _ 1,\cdots, \boldsymbol{s} _ N|\boldsymbol{\pi}) \\ &=p(\boldsymbol{s} _ 1|\boldsymbol{\pi}) \cdots p(\boldsymbol{s} _ N|\boldsymbol{\pi})\\ &= \Pi _ {n=1}^N p(\boldsymbol{s} _ n|\boldsymbol{\pi}) \end{align}

次に $p(\boldsymbol{\Theta})$ であるが，

\begin{align} p(\boldsymbol{\Theta}) &= p(\boldsymbol{\theta} _ 1,\cdots, \boldsymbol{\theta} _ K) \\ &=p(\boldsymbol{\theta} _ 1) \cdots p(\boldsymbol{\theta} _ k)\\ &= \Pi _ {k=1}^K p(\boldsymbol{\theta} _ k) \end{align}

したがって同時分布の式は

\begin{align} p(\boldsymbol{X},\boldsymbol{S},\boldsymbol{\Theta},\boldsymbol{\pi}) &= p(\boldsymbol{X}|\boldsymbol{S},\boldsymbol{\Theta}, \boldsymbol{\pi})p(\boldsymbol{\Theta}|\boldsymbol{S},\boldsymbol{\pi})p(\boldsymbol{S}|\boldsymbol{\pi})p(\boldsymbol{\pi}) \\ &= p(\boldsymbol{X}|\boldsymbol{S},\boldsymbol{\Theta})p(\boldsymbol{\Theta})p(\boldsymbol{S}|\boldsymbol{\pi})p(\boldsymbol{\pi}) \\ &= \left( \Pi _ {n=1}^N p(\boldsymbol{x} _ n|\boldsymbol{s} _ n,\boldsymbol{\Theta}) p(\boldsymbol{s} _ n|\boldsymbol{\pi}) \right) \left( \Pi _ {k=1}^K p(\boldsymbol{\theta} _ k) \right) p(\boldsymbol{\pi}) \end{align}

こうして須山本の式（4.5）に辿り着きました．めでたし．

事後分布

データが所属するクラスタの推定を行いたい場合，事後分布 $p(\boldsymbol{S}|\boldsymbol{X})$ を求めれば良い．

\begin{align} p(\boldsymbol{S}|\boldsymbol{X}) &=\int \int p(\boldsymbol{S},\boldsymbol{\Theta},\boldsymbol{\pi}|\boldsymbol{X}){\rm d}\boldsymbol{\Theta}{\rm d}\boldsymbol{\pi}\\ p(\boldsymbol{S},\boldsymbol{\Theta},\boldsymbol{\pi}|\boldsymbol{X}) &= \frac{p(\boldsymbol{X},\boldsymbol{S},\boldsymbol{\Theta},\boldsymbol{\pi})} {p(\boldsymbol{X})} \end{align}

であるが，この計算は一般に困難とされている．その解決法として，なんらかの近似アルゴリズムによって推論を行おう，ということでMCMCや変分推論に話が繋がっていく．

ギャラクシースーパーはてなブログ

ギャラクシースーパーノヴァ子の日記だお

混合モデルの導入